Lec 2 —— Markov Decision Process

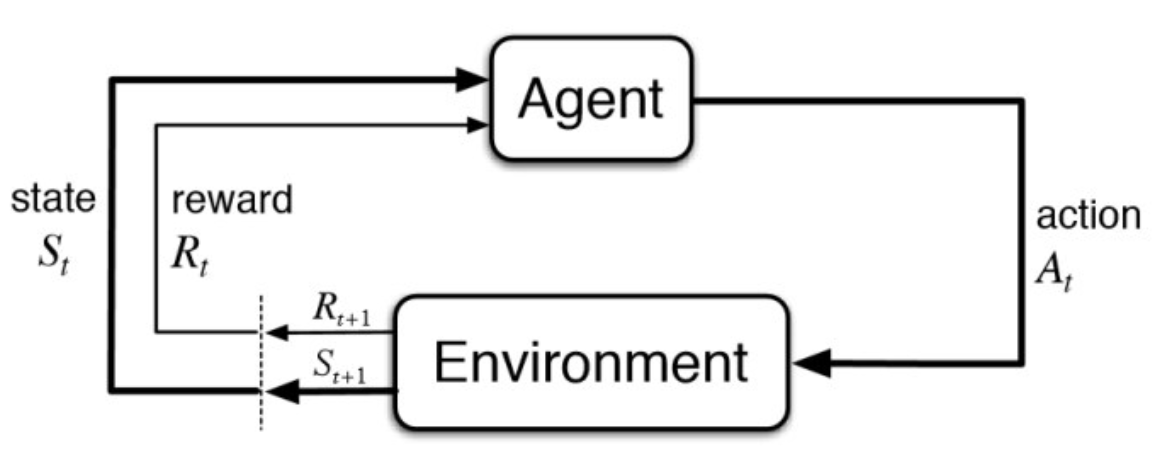
⬆️马尔可夫决策过程

马尔可夫链

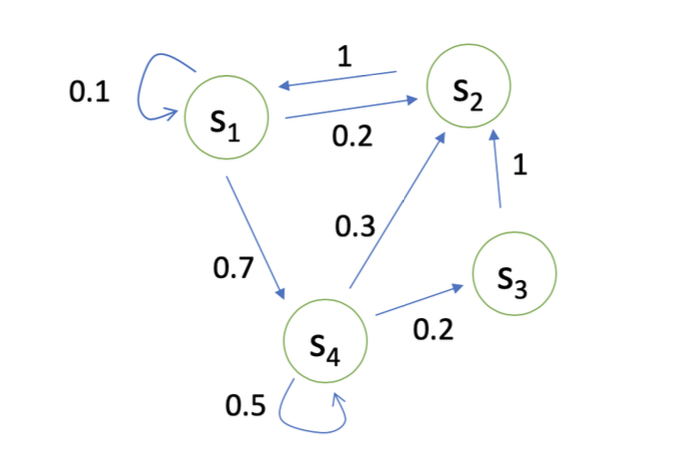
马尔可夫奖励过程

马尔可夫奖励过程 = 马尔可夫链 + 奖励函数

$R(s_{t}=s)=\mathbb{E}[r_{t}|s_{t} = s]$

Return 的定义

Value 函数的定义

$\gamma = 0$: 只关注当前的奖励

$\gamma = 1$: 未来奖励和当前奖励相同

计算马尔可夫奖励过程(MRP)的方法

贝尔曼方程：$V(s) = R(s) + \gamma\sum_{s'\in S}P(s'|s)V(s')$

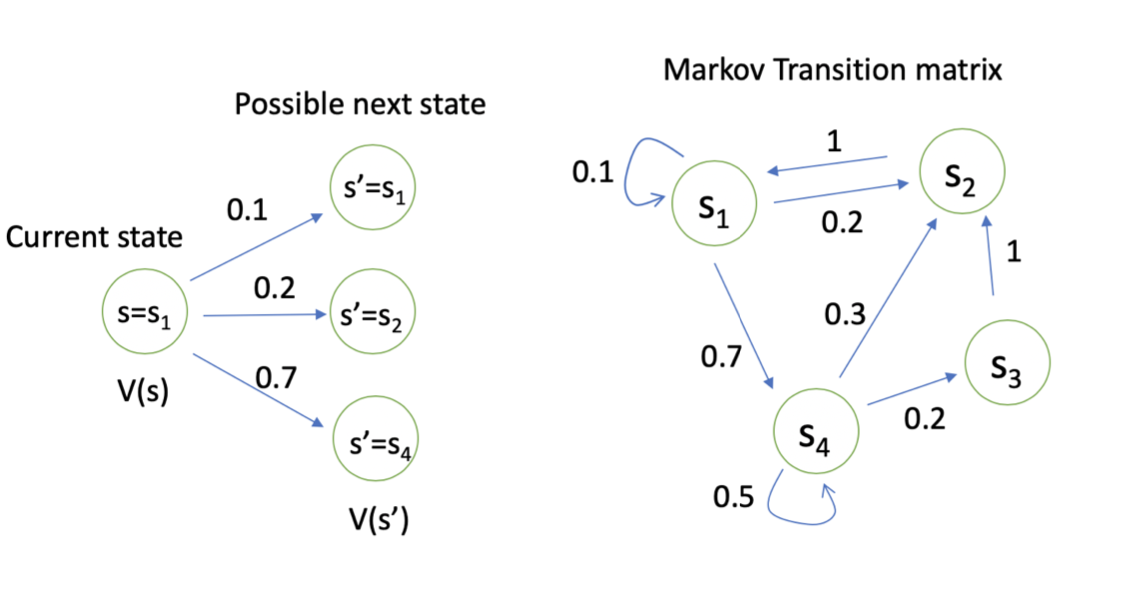
求解大型MRP的方法：

• 动态规划
• 蒙特卡洛（采样）
• Temporal-Difference learning(结合1、2)

蒙特卡洛方法

随机产生多条轨迹，取平均

动态规划方法

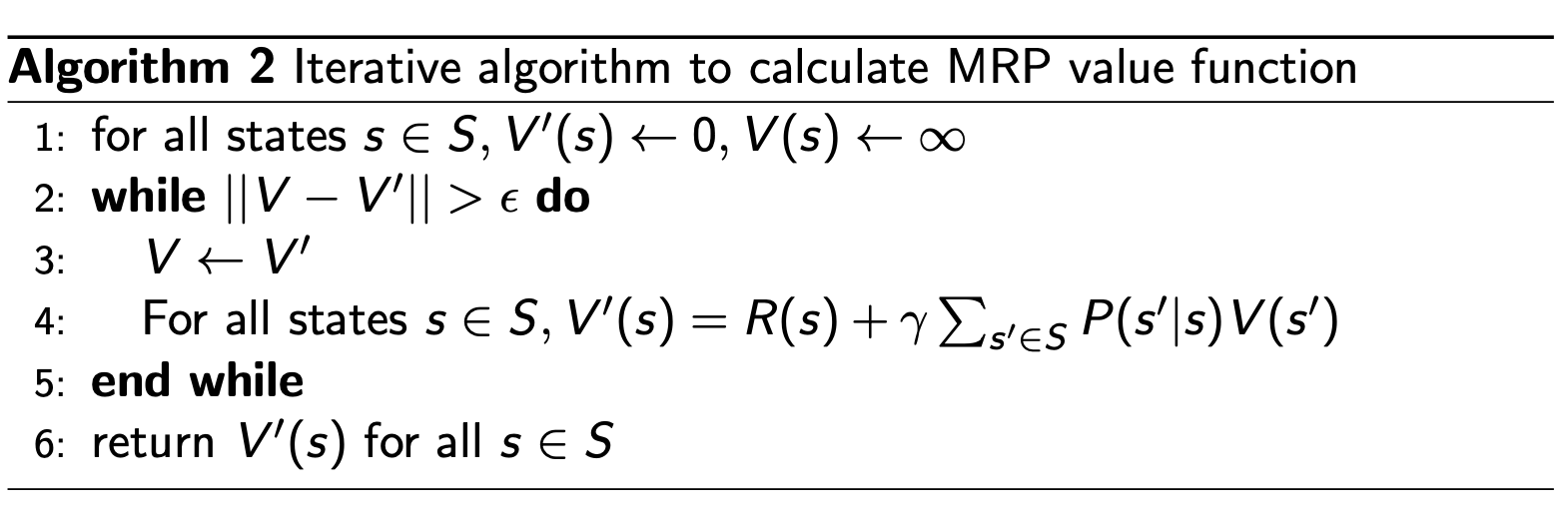
迭代、使收敛

马尔可夫决策过程(MDP)

MDP = MRP + Action

$R(s_{t}=s,a_{t} = a) = \mathbb{E}[r_{t}|s_{t}= s,a_{t} = a]$

MDP 包含（S, A, P, R, $\gamma$）

Policy

$\pi(a|s) = P(a_{t} = a|s_{t} = s)$

给定一个MDP(S, A, P, R, $\gamma$)，和一个策略$\pi$，可以转换为MRP

MDP的Value函数

• state-value func:
• $\mathbb{v}^\pi(s) = \mathbb{E}_{\pi}[G_{t}|s_{t} = s]$
• Action-value func:
• $q^\pi(s,a) = \mathbb{E}_{\pi}[G_{t}|s_{t} = s, A_{t} = a]$
• 于是得到这两个函数的关系:
• $v^\pi(s) = \sum_{a\in A}\pi(a|s)q^\pi(s,a )$

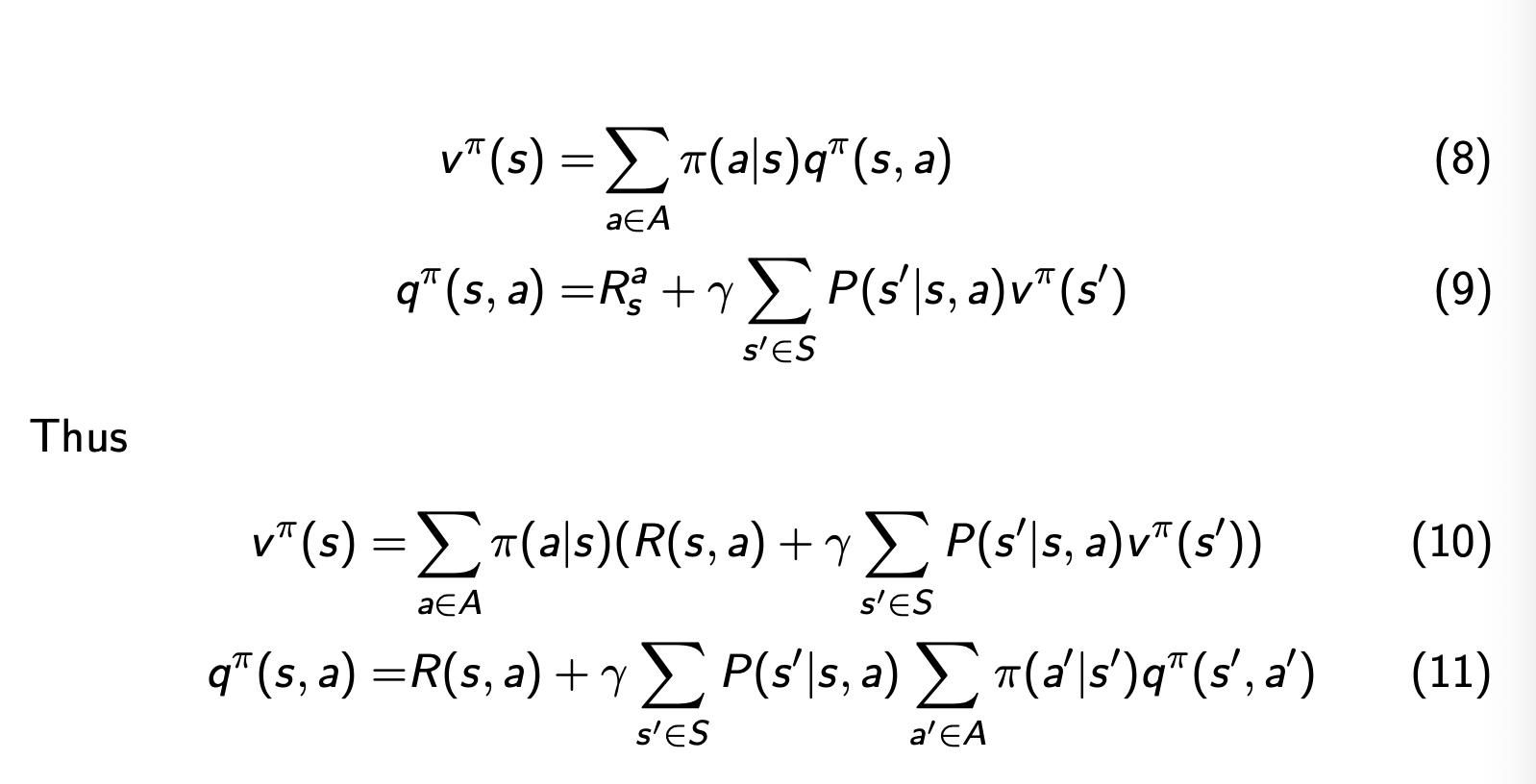
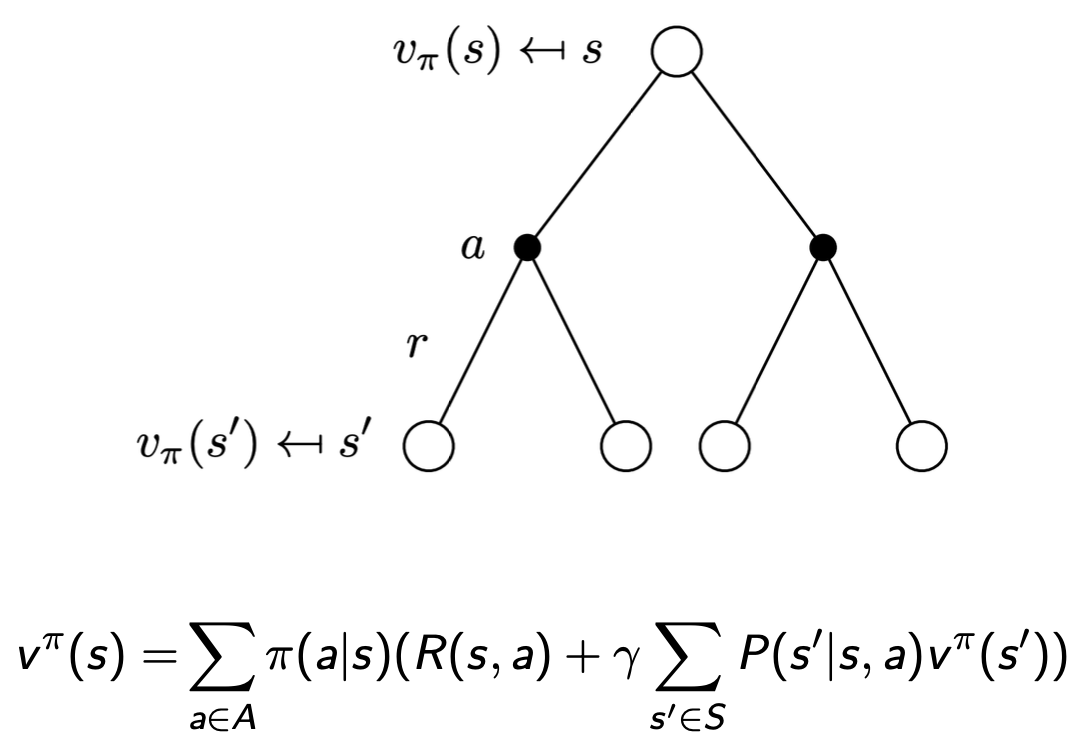
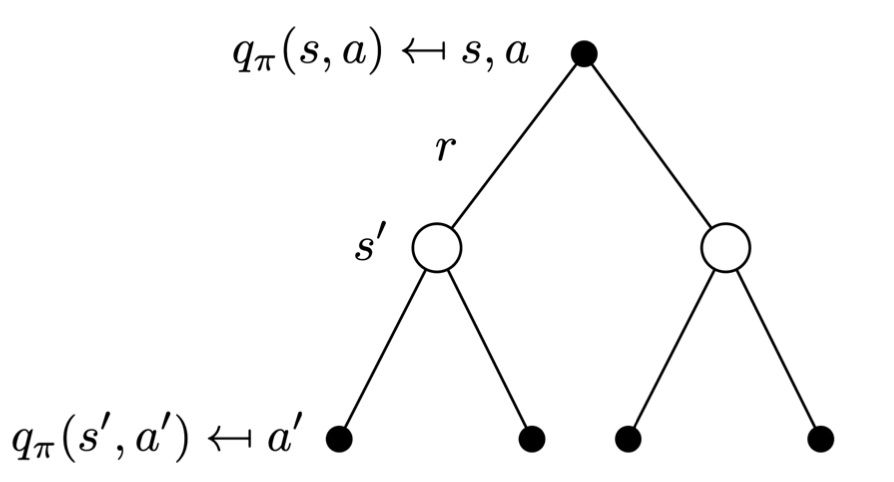
Policy Evalution 评估策略

计算$v^\pi(s)$：与计算$v(s)$的方法类似

MDP中的决策过程

• 预测：输出$v^\pi$
• 搜索最优策略：输出最优$v^*$和$\pi^*$

给定策略

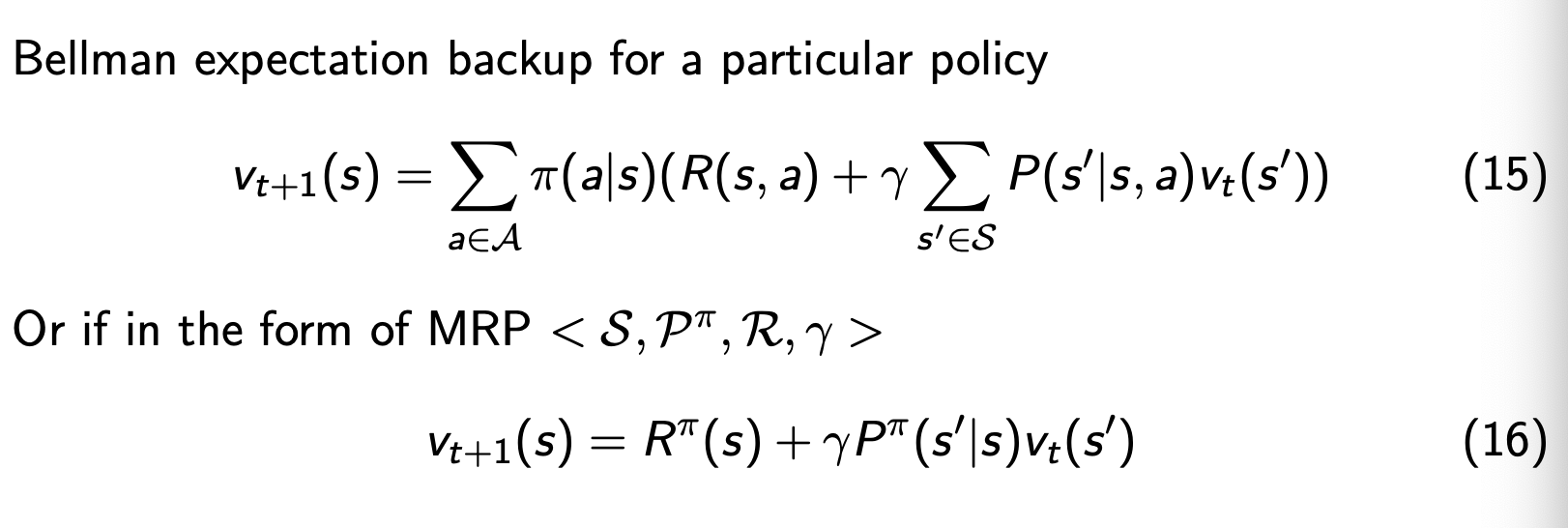
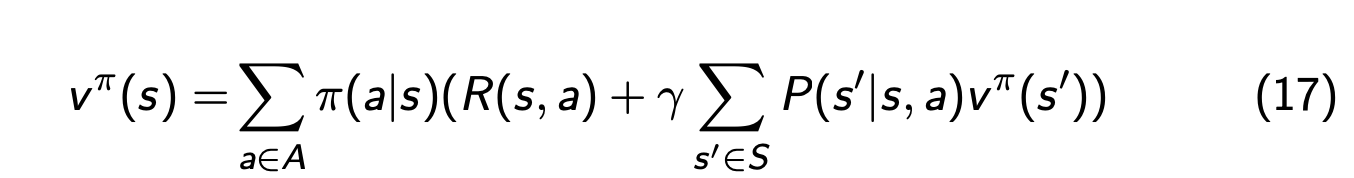
搜索策略

policy iteration

$\pi^*(s) = argmax_{\pi}v^\pi(s)$

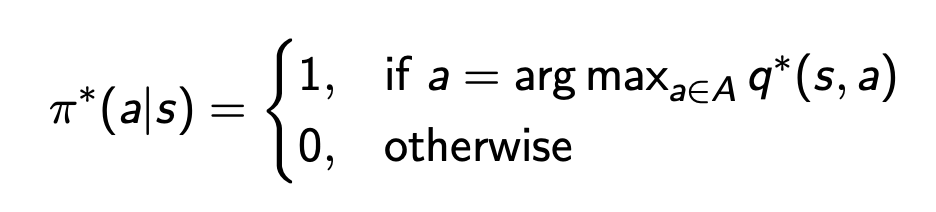
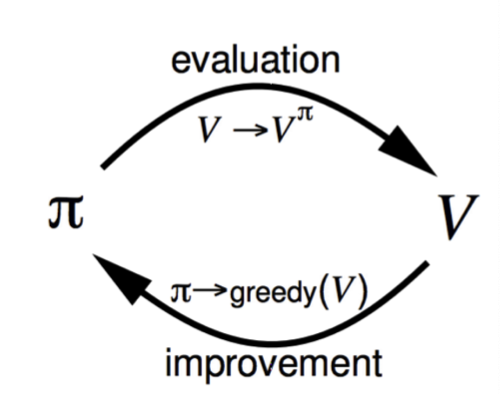
任意选取$\pi$，计算出$v$，根据$v$计算出$q$，然后更新$\pi$

由此可得出最佳的policy

于是当改进停止时，Bellman optimality equation 满足

value iteration

仅仅优化value，最后retrieve policy